2023   01   az   p.44-48 N.B. Agayev, R.H. Hashimov,
Probability-statistical approach to control of chaotic processes		  pdf 

ABSTRACT

Inthearticle, a probabilistic-statistical approach was proposed in the management of complex dynamic changes observed by chaotic and bifurcated movement of self-organization effects in the system as a result of non-linear dynamics and unstable movement of complex systems. The proposed method of the system should be applied in the intervals when the conditions of synchronicity and stability of the system are satisfied.

Keywords: complex system, chaotic processes, unsteady motion, chaotic and bifurcation motion, spatial coordinate of the system, mathematical expectation, probabilistic-statistical approach.
PACS: 05.45.−a, 05.45.Ac, 05.45.Mt, 05.45.Xt

DOI:-

Received: 13.02.2023

AUTHORS & AFFILIATIONS

Azerbaijan Technical University, 25 H. Javid ave., Baku, AZ 1073
E-mail: rasim68az@aztu.edu.az

Graphics and Images

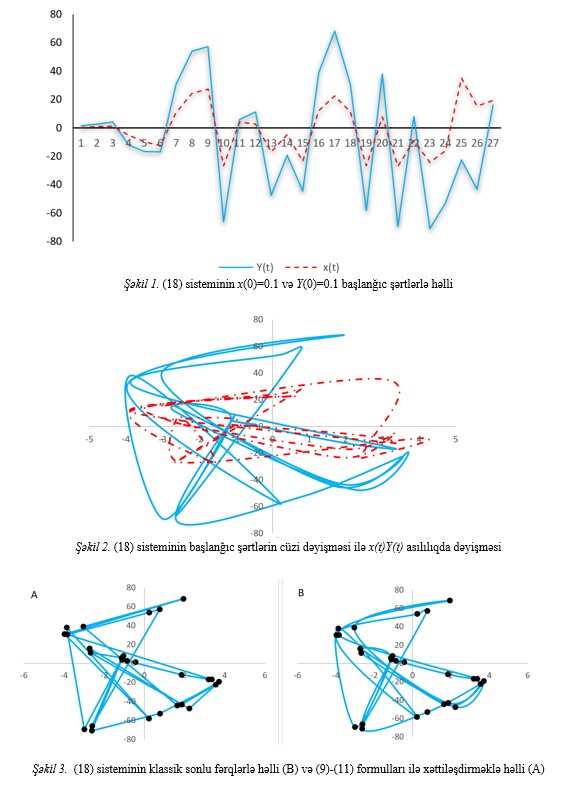
 REFERENCIES

[1]   Г.Г. Малинецкий, А.Б. Потапов. Современ-ные проблемы нелинейной динамики. М., Эдиториал УРСС, 2000.
[2]   Г. Шустер. Детерминированный хаос. М., Мир, 1988.
[3]   А.С. Дмитриев, А.И. Панас. Динамический хаос. Новые носители информации для систем связи. М., Физматгиз, 2002.
[4]   А.Ю. Лоскутов, А.А. Козлов, Ю.М. Хаханов. Прикладная нелинейная динамика, 2009.
[5]   Б.Е. Тайлак. Модель псевдослучайного генератора, построенного на базе хаотической системы: Труды международной научной конференции «Наука и образование – ведущий фактор стратегии «Казахстан – 2030». – Караганда
[6]   Л.Б. Ряшко. Стабилизация стохастически возмущенных нелинейных колебаний. Автоматика и телемеханика, 2007. – № 10
[7]   S. Tung, A. Mishra, S. Dey. Stabilizing the Dynamics of Laboratory Populations of Drosophila Melanogaster Through Upper and Lower Limiter Controls. Ecological complexity, 2016. – doi: 10.1016/j.ecocom.2015, 11, 003.
[8]   Р.В. Беляев, Г.М. Воронцов, В.В. Колесов. Случайные последовательности, формируемые нелинейным алгоритмом с запаздыванием. Радиотехника и электроника, 2000, т. 45, № 12, с. 954–96.
[9]   E.M. Shahverdiev, R.A. Nuriev, L.H. Hashimov, E.M. Huseynova, R.H. Hashimov, K.A. Shore. Completeinverse chaos synchronization, parameter mismatches and generalized synchronization in the multi-feedback Ikeda model. Chaos, Solitons & Fractals.Volume 36, Issue 2, April 2008, p. 211-216.
[10]  E.M. Shahverdiev, R.A. Nuriev, E.M. Huseynova,L.H. Hashimova, R.H.Hashimov. Inverse chaose synchronization in the multi-feedback Ikeda model. Fizika,cild XI, № 1-2, Bakı 2005.
[11]  E.M. Shahverdiev, R.A. Nuriev, R.H. Hashimov. Parameter mismatches and Inverse Synchronization in the Ikeda Model. International Journal of Modern Physics B, vol. 18, № 13, 2004, 1-8.
[12]  E.M. Shahverdiev, R.A. Nuriev, R.H. Hashimov, K.A. Shore. Parameter mismatches, variable delay times and synchronization in time- delayed systems. Chaos, Solitons & Fractals 25, 2005, p. 325-331.